an exercise in archæological algorithmic analysis
Forum rules
This forum is for discussing APL-related issues. If you think that the subject is off-topic, then the Chat forum is probably a better place for your thoughts !
This forum is for discussing APL-related issues. If you think that the subject is off-topic, then the Chat forum is probably a better place for your thoughts !
2 posts
• Page 1 of 1
an exercise in archæological algorithmic analysis
A Scholism describing events from the 1970s:
Al Rose’s feat was all the more impressive because he did it in a first-generation APL. In current Dyalog APL, the computation can be
The modern APL expression uses facilities not available in the 1970s: dfns, the key operator ⌸, nested arrays, a proper indexing function, extensions to grade, and total array ordering.
So how might have Al Rose solve the problem? Let us speculate. But first, let us pause and remember that our solution is composed in quiet calm, not on stage in front of an audience and under time pressure.
A. The Corpus
Perhaps the Book of Psalms is in the form of a character matrix. If not, if (say) in the form of a character vector t with each word preceded by a blank, it would first have to be made into a matrix:
The transformation (the last line) is non-trivial, but was a phrase well-known in the APL milieu sure to be in Rose's repertoire. (In modern APL you’d say ↑' '(≠⊆⊢)t.) The phrase does contain an anachronism because it requires 0-origin indexing, while in those days, before the unrighteousness of variable index origin was realized, the usual practice was 1-origin indexing. ⎕io delenda est!
What about mixed case text? In those days of the italic upper case and italic underscored upper case alphabets and only those alphabets, it seems reasonable that the corpus would be single case. What about punctuation? What about that the entire Book of Psalms was probably too large for a workspace available in those days? What about ... ? Left as exercises for the reader. :-)
B. A Solution
With the character matrix a of the words in hand, the problem can be divided into parts:
(a) Absent an extended ⍳ function, the solution involves sorting and therefore grade. At the time, grade works only on numeric arrays, so here grade is applied to the alphabetical indices of the matrix of words.
(b) Find the places b where a sorted row differs from the preceding row. These mark the unique rows.
(c) Find the indices i of these rows. From that find by how much an index differs from the preceding index. These give the number of occurrences c of each sorted row.
(d) Grade the occurrences in decreasing order.
(e) Index the sorted rows by this grade, and likewise index the corresponding number of occurrences. For the output, using ⍕, the occurrences must be made into a 1-column matrix, complicated by that ⍪ was not available (i.e. c[((⍴j),1)⍴j] instead of the modern c[⍪j] or ⍪c[j]).
You may note that the output differs from the output above. The reason is that in the key solution above ties in the number of occurrences are resolved in favor of the alphabetically greater word, whereas here they are resolved in favor of the alphabetically lesser word.
A final sanity check: in a typical English corpus it is known that “the” would be the most frequently occurring word.
Al Rose was one of the best stage acts I can remember. I attended a gig of his somewhere in London in the early ’70s. Al had an IBM golf-ball APL terminal. As a finale, he said, “I have The Book of Psalms here — what do you want to know?” There was a long pause, until someone in the audience asked, “Which word occurs most often?”
Al put his head down and thought for around a minute (which is a very, very long time when you’re on stage). Then he typed in a fairly long APL expression. There was a pause. Then the typewriter started clattering out a list of the unique words and their counts in order of frequency. It brought the house down.
The best thing about the experience was the look on the FORTRAN programmers’ faces :-)
Al Rose’s feat was all the more impressive because he did it in a first-generation APL. In current Dyalog APL, the computation can be
⌽ {(⊂⍒⍵)⌷⍵} {(≢⍵)⍺}⌸ a
the 7
me 7
of 6
my 6
in 5
i 4
he 4
you 3
will 3
and 3
your 2
with 2
lord 2
for 2
waters 1
want 1
...The modern APL expression uses facilities not available in the 1970s: dfns, the key operator ⌸, nested arrays, a proper indexing function, extensions to grade, and total array ordering.
So how might have Al Rose solve the problem? Let us speculate. But first, let us pause and remember that our solution is composed in quiet calm, not on stage in front of an audience and under time pressure.
A. The Corpus
Perhaps the Book of Psalms is in the form of a character matrix. If not, if (say) in the form of a character vector t with each word preceded by a blank, it would first have to be made into a matrix:
t← ' the lord is my shepherd i shall not be in want'
t←t,' he makes me lie down in green pastures'
t←t,' he leads me beside quiet waters'
t←t,' he restores my soul'
t←t,' he guides me in paths of righteousness for his names sake'
t←t,' even though i walk through the valley of the shadow of death'
t←t,' i will fear no evil'
t←t,' for you are with me your rod and your staff they comfort me'
t←t,' you prepare a table before me in the presence of my enemies'
t←t,' you anoint my head with oil my cup overflows'
t←t,' surely goodness and love will follow me all the days of my life'
t←t,' and i will dwell in the house of the lord forever'
a← 0 1↓ ((⍴k),m) ⍴ (,k∘.>⍳m←⌈/k←(1↓i,⍴t)-i←(' '=t)/⍳⍴t) \ t
The transformation (the last line) is non-trivial, but was a phrase well-known in the APL milieu sure to be in Rose's repertoire. (In modern APL you’d say ↑' '(≠⊆⊢)t.) The phrase does contain an anachronism because it requires 0-origin indexing, while in those days, before the unrighteousness of variable index origin was realized, the usual practice was 1-origin indexing. ⎕io delenda est!
What about mixed case text? In those days of the italic upper case and italic underscored upper case alphabets and only those alphabets, it seems reasonable that the corpus would be single case. What about punctuation? What about that the entire Book of Psalms was probably too large for a workspace available in those days? What about ... ? Left as exercises for the reader. :-)
B. A Solution
With the character matrix a of the words in hand, the problem can be divided into parts:
- find the unique words
- find the number of occurrences of each unique word
- find the word(s) with the maximum number of occurrences
A←'abcdefghijklmnopqrstuvwxyz'
s←a[⍋(' ',A)⍳a;] ⍝ (a)
b←∨/s≠¯1 0↓' ',[0]s ⍝ (b)
c←i-¯1↓¯1,i←b/⍳⍴b ⍝ (c)
j←⍒c ⍝ (d)
(b⌿s)[j;], ⍕c[((⍴j),1)⍴j] ⍝ (e)
me 7
the 7
my 6
of 6
in 5
he 4
i 4
and 3
will 3
you 3
for 2
lord 2
with 2
your 2
a 1
all 1
...
(a) Absent an extended ⍳ function, the solution involves sorting and therefore grade. At the time, grade works only on numeric arrays, so here grade is applied to the alphabetical indices of the matrix of words.
(b) Find the places b where a sorted row differs from the preceding row. These mark the unique rows.
(c) Find the indices i of these rows. From that find by how much an index differs from the preceding index. These give the number of occurrences c of each sorted row.
(d) Grade the occurrences in decreasing order.
(e) Index the sorted rows by this grade, and likewise index the corresponding number of occurrences. For the output, using ⍕, the occurrences must be made into a 1-column matrix, complicated by that ⍪ was not available (i.e. c[((⍴j),1)⍴j] instead of the modern c[⍪j] or ⍪c[j]).
You may note that the output differs from the output above. The reason is that in the key solution above ties in the number of occurrences are resolved in favor of the alphabetically greater word, whereas here they are resolved in favor of the alphabetically lesser word.
A final sanity check: in a typical English corpus it is known that “the” would be the most frequently occurring word.
- Roger|Dyalog
- Posts: 238
- Joined: Thu Jul 28, 2011 10:53 am
Re: an exercise in archæological algorithmic analysis
Roger ,
I can't help but take your bit of history as a challenge . Particularly because the essential verb is extremely useful and I know has a rich history . But I've never implemented it in a general form . In K it is monadic = .
Here's what it all looks like in CoSy . I'll admit it took me all yesterday afternoon & evening .
First because your listing of Psalm 23 has a lot of noise , I googled it and copied it into the ` res window and from there into a persistent ( ie: saved with environment aka ` workspace ) variable .
Then cleaned it up and converted to a list of lower case words .
Skipping all the experiments and wrong thoughts to get to the result
And because what's frequently wanted is both the nub and the index histogram I made
to save needing a redundant ' nub .
So , we now have
Where ' flip is obviously transpose and is just between 2 ` dimensions like K .
I think it informative to point out a couple of the verbs .
which returns the script where nub is defined and the definition . Note that there are 3 versions . There are a number of similar families of words .
The final word I want to mention is ' where used in the basic ' nubb
The reason I mention it is the use of the adverb ' f? . It's the same thing as diadic ⍳ , K's ` ? , but generalized to an adverb taking a boolean verb as the test on list items .
Note the simplicity of ` operators taking functions , verbs , as arguments because of Forth's minimal RPN syntax and , since working directly with chip memory addresses , the word ' putting the address of the next word , whatever it may be , on the stack .
Oops almost forgot the final step : the counts rather than the indices .
I'll do somewhat round about
Curiously , I've never settled on adding a ' sort to my vocabulary -- largely because I so want APL's ` grade -- which have figured out how to do using Helmar Wodtke's brilliant algorithm -- that I've never got back to finishing .
| PS: 20200428.1037| A final comment on the use of ' swap above .
It's Forth's equivalent to commute . It exchanges the top 2 items on the stack .
-- |
Anyway , useful to have been challenged by this . Don't think I ever met Rose .
Below is a screen shot which should help explain the screen scraping and copying from the web source I grabbed .
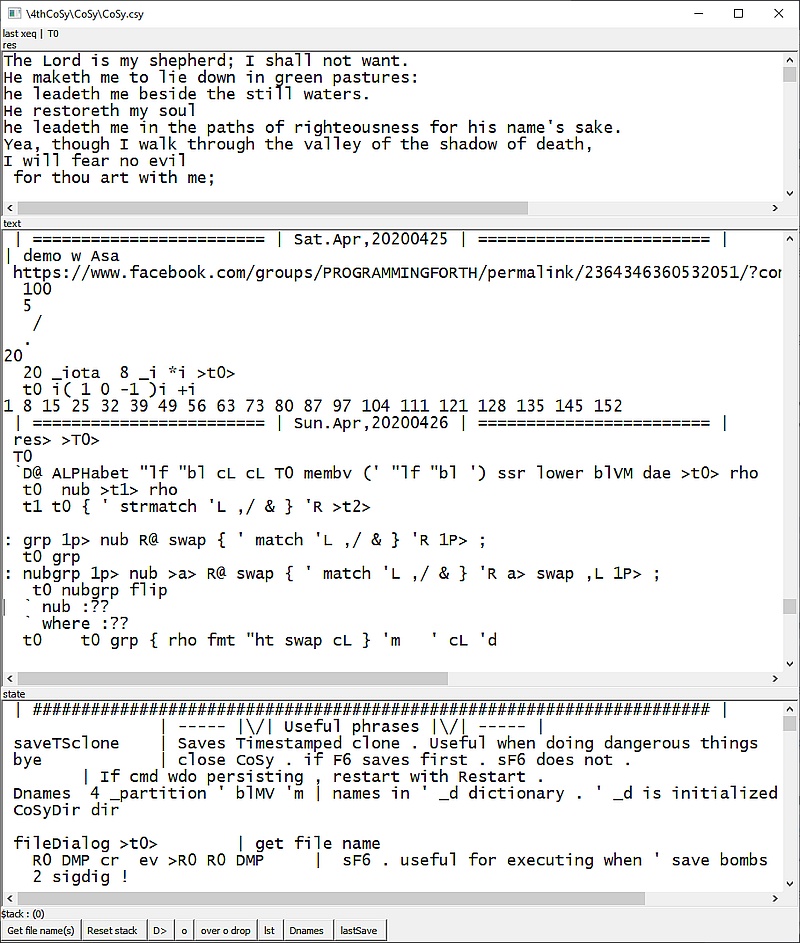
I can't help but take your bit of history as a challenge . Particularly because the essential verb is extremely useful and I know has a rich history . But I've never implemented it in a general form . In K it is monadic = .
Here's what it all looks like in CoSy . I'll admit it took me all yesterday afternoon & evening .
First because your listing of Psalm 23 has a lot of noise , I googled it and copied it into the ` res window and from there into a persistent ( ie: saved with environment aka ` workspace ) variable .
- Code: Select all
res> >T0
Then cleaned it up and converted to a list of lower case words .
- Code: Select all
`D@ ALPHabet "lf "bl cL cL T0 membv (' "lf "bl ') ssr lower blVM dae >t0> rho
118
Skipping all the experiments and wrong thoughts to get to the result
- Code: Select all
| return list of indices of occurrences of each unique item of list .
: grp 1p> nub R@ swap { ' match 'L ,/ & } 'R 1P> ;
t0 grp
(
0 22 33 46 49 78 101 111 114
1 115
2
3 27 85 89 104
4
5 43 53 107
6 97
7
...
)
And because what's frequently wanted is both the nub and the index histogram I made
- Code: Select all
| returns 2 item list of unique items and their indices .
: nubgrp 1p> nub >a> R@ swap { ' match 'L ,/ & } 'R a> swap ,L 1P> ;
to save needing a redundant ' nub .
So , we now have
- Code: Select all
t0 nubgrp flip
(
(
the
0 22 33 46 49 78 101 111 114
) (
lord
1 115
) (
is
2
) (
my
3 27 85 89 104
) (
shepherd
4
) (
i
5 43 53 107
) ( ...
Where ' flip is obviously transpose and is just between 2 ` dimensions like K .
I think it informative to point out a couple of the verbs .
- Code: Select all
` nub :??
(
./CoSy/CoSy.f
| return unique items . Like K's ' ?
: nubb 1p> R@ ['] where 'R ,/ R@ rho iota =i 1P> ; | bool of 1st occurrences
: nubx nubb & ; | indices of 1st occurances
: nub 1p> dup nubx at 1P> ; | unique items .
...
which returns the script where nub is defined and the definition . Note that there are 3 versions . There are a number of similar families of words .
The final word I want to mention is ' where used in the basic ' nubb
- Code: Select all
: where ( l v -- idx ) ' match f? ;
| Index of first item in L on which bool verb is true . count of L if not found .
The reason I mention it is the use of the adverb ' f? . It's the same thing as diadic ⍳ , K's ` ? , but generalized to an adverb taking a boolean verb as the test on list items .
Note the simplicity of ` operators taking functions , verbs , as arguments because of Forth's minimal RPN syntax and , since working directly with chip memory addresses , the word ' putting the address of the next word , whatever it may be , on the stack .
Oops almost forgot the final step : the counts rather than the indices .
I'll do somewhat round about
- Code: Select all
t0 t0 grp { rho fmt "ht swap cL } 'm ' cL 'd
(
the 9
lord 2
is 1
my 5
shepherd 1
i 4
shall 2
...
Curiously , I've never settled on adding a ' sort to my vocabulary -- largely because I so want APL's ` grade -- which have figured out how to do using Helmar Wodtke's brilliant algorithm -- that I've never got back to finishing .
| PS: 20200428.1037| A final comment on the use of ' swap above .
- Code: Select all
` swap See
89 C3 mov ebx,eax
8B 06 mov eax,[esi]
89 1E mov [esi],ebx
C3 ret
It's Forth's equivalent to commute . It exchanges the top 2 items on the stack .
-- |
Anyway , useful to have been challenged by this . Don't think I ever met Rose .
Below is a screen shot which should help explain the screen scraping and copying from the web source I grabbed .

-

Bob Armstrong - Posts: 26
- Joined: Wed Dec 23, 2009 8:41 pm
- Location: 39.038681° -105.079070° 2500m
2 posts
• Page 1 of 1
Who is online
Users browsing this forum: No registered users and 1 guest
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
